Logarithms and Exponentials

What is the relationship and differences between logarithms and exponentials?

They are fundamentally linked. Logarithms are the inverse operation of exponentiation.

They are two sides of the same coin, describing the same relationship between a base, an exponent, and a result, just from different perspectives.

Think of it like addition and subtraction, or multiplication and division. One undoes the other.

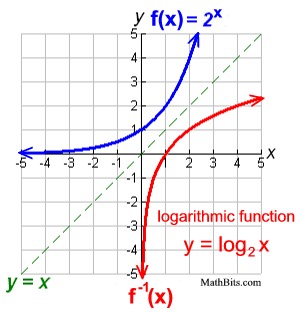
Exponential Functions

1. They are functions where a constant base is raised to a variable exponent.
2. Form: y = b^x
   1. e.g. 8 = 2^3
   2. b is the constant base (b > 0, b ≠ 1)
   3. x is the variable exponent
   4. y is the result
3. Purpose:
   1. Describes rapid growth (if b > 1) or decay (if 0 < b < 1).
   2. Answers the question: “If I start with a base b and multiply it by itself x times, what result y do I get?”
4. Example: y = 2^3
   1. Base b = 2
   2. Exponent x = 3
   3. Result y = 2 * 2 * 2 = 8
5. Key Characteristics:
   1. Domain: All real numbers (x can be anything)
   2. Range: y > 0 (The result is always positive)
   3. Graph: Passes through the point (0, 1) because b^0 = 1. Has a horizontal asymptote at y = 0 (the x-axis). Grows very quickly (for b > 1).

Logarithmic Functions

1. They are the inverse of exponential functions. They find the exponent.
2. Form: x = log_b(y) (read as “log of y with base b equals x”)
   1. e.g. log 8(2) = 3
   2. b is the base (b > 0, b ≠ 1) - same base as the corresponding exponential
   3. y is the argument (the number you’re taking the log of, which corresponds to the result of the exponential function) (y > 0)
   4. x is the result (which corresponds to the exponent in the exponential function)
3. Purpose:
   1. Answers the question: “To what exponent x must I raise the base b to get the number y?”
   2. In other words, how many times do I have to cut down y (by base b) to reach x?
   3. “8” has to be cut down “3” times by base “2”.
4. Relationship to Exponential: The statement y = b^x is exactly equivalent to x = log_b(y).
5. Example: log_2(8) = x
   1. This asks: “To what power (x) must I raise the base 2 to get 8?”
   2. Since 2^3 = 8, the answer is x = 3.
   3. So, log_2(8) = 3.
6. Key Characteristics (often written as y = log_b(x) for function analysis):
   1. Domain: x > 0 (You can only take the logarithm of a positive number)
   2. Range: All real numbers (y can be anything)
   3. Graph: Passes through the point (1, 0) because log_b(1) = 0 (since b^0 = 1). Has a vertical asymptote at x = 0 (the y-axis). Grows very slowly.

Comparison Summary

Feature	Exponential Function (y = b^x)	Logarithmic Function (y = log_b(x))
Relationship	Finds the result given a base and exponent	Finds the exponent given a base and result
Inverse Of	Logarithmic Function	Exponential Function
Standard Form	y = b^x	y = log_b(x)
Variable is	Exponent (x)	Argument (x)
Output is	Result of exponentiation (y)	The required exponent (y)
Domain	All real numbers ((-∞, ∞))	Positive real numbers ((0, ∞))
Range	Positive real numbers ((0, ∞))	All real numbers ((-∞, ∞))
Key Point	Passes through (0, 1)	Passes through (1, 0)
Asymptote	Horizontal (y = 0)	Vertical (x = 0)
Growth Rate	Very fast (accelerating for b > 1)	Very slow (decelerating)
Example	8 = 2^3	3 = log_2(8)

In Essence

1. Exponentials scale things up (or down) very quickly based on the exponent.
2. Logarithms scale things down, allowing us to deal with numbers that grow extremely large by focusing on their exponents. They are useful for measuring things that vary over huge ranges (like earthquake intensity - Richter scale, sound intensity - decibels, acidity - pH scale).

Reading material

https://mathbitsnotebook.com/Algebra2/Exponential/EXLogFunctions.html