Priority Queue Data Structure or Heap Data Structure
Priority Queues
Source: Skiena
Many algorithms process items in a specific order. For example, suppose you must schedule jobs according to their importance relative to other jobs. Scheduling the jobs requires sorting them by importance, and then evaluating them in this sorted order.
Priority queues are data structures that provide more flexibility than simple sorting, because they allow new elements to enter a system at arbitrary intervals. It is much more cost-effective to insert a new job into a priority queue than to re-sort everything on each such arrival.
The basic priority queue supports three primary operations:
- Insert(Q,x)– Given an item x with key k, insert it into the priority queue Q.
- Find-Minimum(Q) or Find-Maximum(Q)– Return a pointer to the item whose key value is smaller (larger) than any other key in the priority queue Q.
- Delete-Minimum(Q) or Delete-Maximum(Q)– Remove the item from the priority queue Q whose key is minimum (maximum).
Many naturally occurring processes are accurately modeled by priority queues. Single people maintain a priority queue of potential dating candidates—mentally if not explicitly. One’s impression on meeting a new person maps directly to an attractiveness or desirability score. Desirability serves as the key field for inserting this new entry into the “little black book” priority queue data structure. Dating is the process of extracting the most desirable person from the data structure (Find- Maximum), spending an evening to evaluate them better, and then reinserting them into the priority queue with a possibly revised score.
What are the applications of Heap Data Structure?
https://www.geeksforgeeks.org/dsa/applications-of-heap-data-structure/
Heap Data Structure is generally taught with Heapsort. Heapsort algorithm has limited uses because Quicksort is better in practice. Nevertheless, the Heap data structure itself is enormously used.
- Priority Queues: Heaps are commonly used to implement priority queues, where elements with higher priority are extracted first. This is useful in many applications such as scheduling tasks, handling interruptions, and processing events.
- Sorting Algorithms: Heapsort, a comparison-based sorting algorithm, is implemented using the Heap data structure. It has a time complexity of O(n log n), making it efficient for large datasets.
- Graph algorithms: Heaps are used in graph algorithms such as Prim’s Algorithm, Dijkstra’s algorithm., and the A* search algorithm.
- Lossless Compression: Heaps are used in data compression algorithms such as Huffman coding, which uses a priority queue implemented as a min-heap to build a Huffman tree.
- Medical Applications: In medical applications, heaps are used to store and manage patient information based on priority, such as vital signs, treatments, and test results.
- Load balancing: Heaps are used in load balancing algorithms to distribute tasks or requests to servers, by processing elements with the lowest load first.
- Order statistics: The Heap data structure can be used to efficiently find the kth smallest (or largest) element in an array. See method 4 and 6 of this post for details.
- Resource allocation: Heaps can be used to efficiently allocate resources in a system, such as memory blocks or CPU time, by assigning a priority to each resource and processing requests in order of priority.
- Job scheduling: The heap data structure is used in job scheduling algorithms, where tasks are scheduled based on their priority or deadline. The heap data structure allows efficient access to the highest-priority task, making it a useful data structure for job scheduling applications.
Heap (data structure)
https://en.wikipedia.org/wiki/Heap_(data_structure)
Heaps are crucial in algorithms like Heapsort and priority queues.
In computer science, a heap is a specialized tree-based data structure which is essentially an almost complete tree that satisfies
the heap property.
The heap is one maximally efficient implementation of an abstract data type called a priority queue, and in fact, priority queues are often referred to as “heaps”, regardless of how they may be implemented.
However, a heap is not a sorted structure; it can be regarded as being partially ordered. A heap is a useful data structure when it is necessary to repeatedly remove the object with the highest (or lowest) priority.
Representation
Heaps are typically implemented using arrays, which makes managing parent-child relationships straightforward.
https://www.geeksforgeeks.org/dsa/array-representation-of-binary-heap/
The traversal method use to achieve Array representation is Level Order Traversal.
https://www.geeksforgeeks.org/dsa/level-order-tree-traversal/
Important formulae
Heaps are typically implemented using an array for efficiency, where for a node at index i:
- Left child is at index
2i + 1 - Right child is at index
2i + 2 - Parent is at index
floor((i-1)/2)
22
/ \
19 18
/ \ / \
15 3 14 4
/
12
Array : [22, 19, 18, 15, 3, 14, 4, 12]
Array position: [0, 1, 2, 3, 4, 5, 6, 7]
For the node at array[i] -
left child = 2i + 1
right child = 2i + 2
parent = floor((i - 1)/2)
The Heap property
This property states that if ‘A’ is a parent node of ‘B’, then the priority of ‘A’ is greater than or equal to the priority of ‘B’.
In a max heap, for any given node C, if P is a parent node of C, then the key (the value) of P is greater than or equal to the key of C.
In a min heap, the key of P is less than or equal to the key of C. The node at the “top” of the heap (with no parents) is called the root node.
In a heap, the highest (or lowest) priority element is always stored at the root.
In a Max-Heap, the parent node is always greater than or equal to its child nodes. The root node is the largest element in the heap.
In a Min-Heap, the parent node is always less than or equal to its child nodes. The root node is the smallest element in the heap.
Min Heap
A Min-Heap is a Data Structure with the following properties.
- It is a complete Complete Binary Tree (See Binary Trees)
- The value of the root node must be the smallest among all its descendant nodes and the same thing must be done for its left and right sub-tree also.
Operations on a Heap
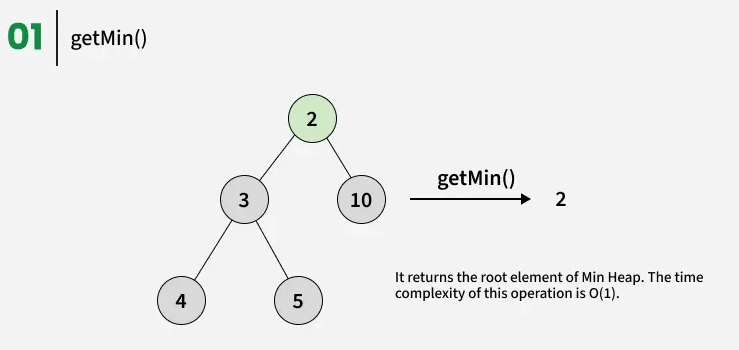
Get Min (a.k.a Peek)
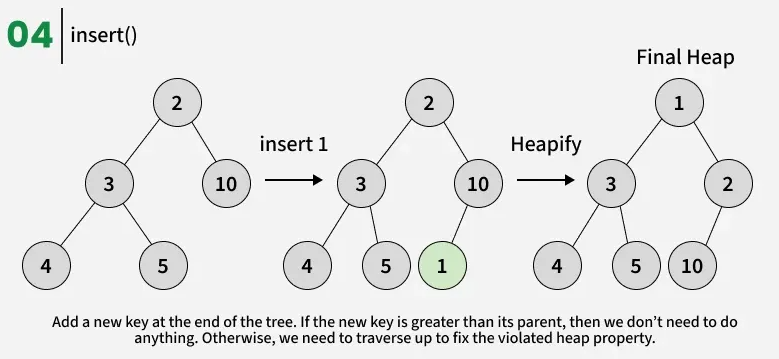
Insert
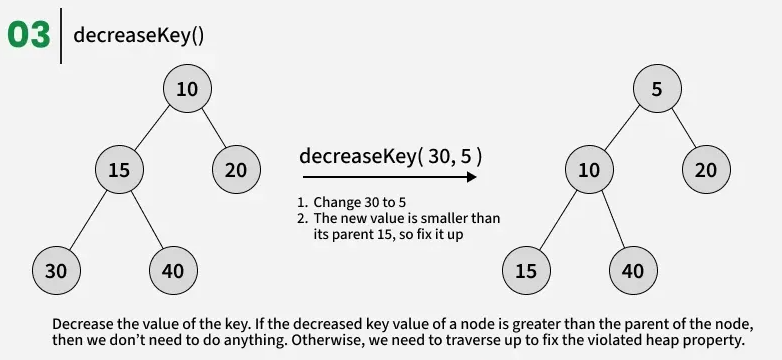
Decrease key
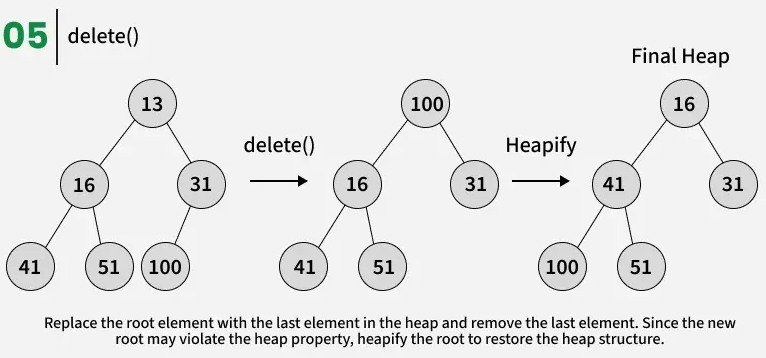
Delete
Extract Min (a.k.a RemoveRoot)
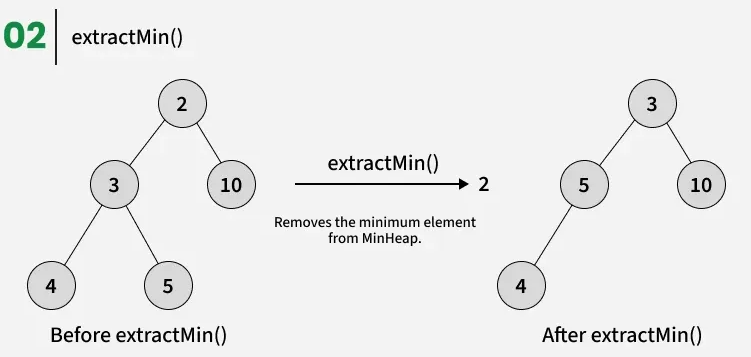
Other common operations involving heaps are:
Min-Heap Example
Let’s start with an empty Min-Heap and insert some elements: [5, 12, 3, 10, 15, 7]
Initial State: [] (empty array)
1. Insert 5:
- Add 5:
[5] - No bubbling up needed.
Heap: [5]
2. Insert 12:
- Add 12:
[5, 12] - 12 is greater than its parent 5. No bubbling up.
Heap: [5, 12]
3. Insert 3:
- Add 3:
[5, 12, 3] - Current index = 2, value = 3. Parent index = (2-1)/2 = 0, parent value = 5.
- 3 < 5, so swap 3 and 5:
[3, 12, 5] - Current index = 0. Stop (reached root).
Heap: [3, 12, 5]
4. Insert 10:
- Add 10:
[3, 12, 5, 10] - Current index = 3, value = 10. Parent index = (3-1)/2 = 1, parent value = 12.
- 10 < 12, so swap 10 and 12:
[3, 10, 5, 12] - Current index = 1. Parent index = (1-1)/2 = 0, parent value = 3.
- 10 > 3. Stop.
Heap: [3, 10, 5, 12]
5. Insert 15:
- Add 15:
[3, 10, 5, 12, 15] - Current index = 4, value = 15. Parent index = (4-1)/2 = 1, parent value = 10.
- 15 > 10. Stop.
Heap: [3, 10, 5, 12, 15]
6. Insert 7:
- Add 7:
[3, 10, 5, 12, 15, 7] - Current index = 5, value = 7. Parent index = (5-1)/2 = 2, parent value = 5.
- 7 > 5. Stop.
Heap: [3, 10, 5, 12, 15, 7]
Now, let’s extractMin from the final heap: [3, 10, 5, 12, 15, 7]
1. Extract min_element:
min_element = 3- Replace root (3) with last element (7):
[7, 10, 5, 12, 15] - Remove last element (original 7):
[7, 10, 5, 12, 15](array size decreased) - Current index = 0, value = 7.
2. Bubble down 7: (a.k.a SinkDown)
-
Left child of 7 (index 1) is 10.
-
Right child of 7 (index 2) is 5.
-
Smallest child is 5 (at index 2).
-
7 > 5, so swap 7 and 5:
[5, 10, 7, 12, 15] -
Current index = 2, value = 7.
-
Left child of 7 (index 5 - out of bounds).
-
Right child of 7 (index 6 - out of bounds).
-
No children or both children are larger. Stop.
Extracted: 3
Final Heap: [5, 10, 7, 12, 15]
Reading material
- Implementation, Explanation - http://www.sourcetricks.com/2011/06/c-heaps.html#.U9z8J_mSzfc
- Tutorial - http://pages.cs.wisc.edu/~vernon/cs367/notes/11.PRIORITY-Q.html
- Implementation - http://www.cprogramming.com/tutorial/computersciencetheory/heapcode.html
- Problem - http://www.codechef.com/problems/REVERSE
- Chapter from CLRS -